Modelling a photon presents a number of challenges. In quantum physics, a photon flies through the air like a wave. They diffract around corners like a wave. Photons interact with each other like waves. Sometimes they reinforce each other, sometimes they interfere and seem to disappear.

The classical explanation uses Maxwell’s equations to describe the wave nature of light. Light waves have perpendicular magnetic and electrical fields that vary in a periodic nature over time. Since the modes of an electromagnetic field have the same classical equations as a simple harmonic oscillator, a photon can and is modeled as a simple harmonic oscillator, where the energy of the photon is proportional to the frequency of the photon. This is commonly known as the first quantization.

Energy as a Harmonic Oscillator

A simple harmonic oscillator is anything with a restoring potential. The simplest examples are things like a spring, or a string with tension, or a wave. In 1926, an Austrian physicist Erwin Schrödinger, described mathematically how a harmonic oscillator stores energy and how to calculate how much energy it stores. The Schrödinger equation describes the system’s “wave function” or “state”, a condition that changes over time on a periodic basis.

For the photon, the value of this restoring potential is known as the Planck constant (h). Planck’s constant, relates the amount of energy stored in a photon to its wavelength (λ). Put another way, Planck’s constant tells you the amount of time it takes the photon to undergo one cycle of whatever its doing given that the photon has a specific amount of energy. The equation E for energy = h / λ, tells us that a photon with low energy will take much longer to complete one cycle of the wave then a photon with high energy.

We start the model of photon phase with a simple harmonic oscillator. Consider a photon model as an expanding and contracting bubble flying through the air at the speed of light. The energy stored in the harmonic oscillator is inversely proportional to the speed of the oscillation. Click to play the photon oscillator game. Watch higher energy photons expand and contract quickly, low energy photons take much longer to go through through a single cycle. The color of a photon depends on its energy and over time, different color photons will get out of phase with each other. Modelling the photon as a simple harmonic oscillator is what Planck had in mind when he proposed the quantization of the energy in oscillators.

The Photon as a Moving Harmonic Oscillator

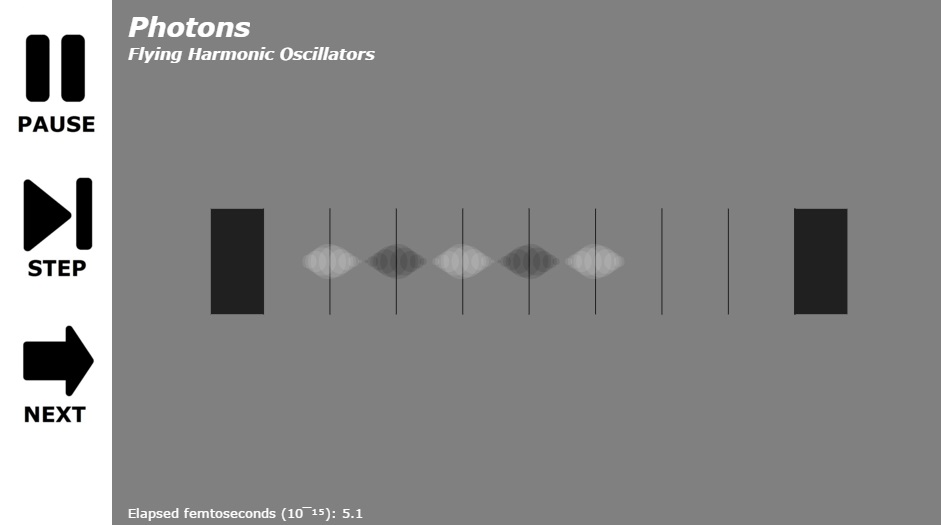
The second quantization deals with multiple copies (ie. integer numbers of excitation’s) of these harmonic oscillators. Each oscillator stores a specific amount of energy and if you split the oscillator, you end up with two oscillators (photons), each of which has 1/2 the energy of the original oscillator (photon). The next step is to put these photons in motion and watch them interact with each other in a small cavity over a period of time.

Modeling the photons as oscillating between a dark state and a light state makes it easy for the animator to illustrate wave reinforcement and wave interference. Click to bounce photons around in a photon cavity. By making the photon somewhat see-through, the “white” phase tends to reinforce other photons in the “white” phase making two “white” photons look even “whiter”. “Dark” photons tend to interfere with “white” photons and the pair simply disappear in the background gray color. “Dark” photons will also reinforce other “dark” photons making for very “dark” spots against the background gray color.

The animation starts with a single 630 nanometer photon (1.97 eVolts) bouncing back and forth in a reflective cavity four wavelengths wide (2,520 nanometers). Releasing additional photons at a rate of 2.1 femtoseconds per photon, produces some interesting interference with one photon per wavelength. Releasing additional photons at the rate of 0.1 femtoseconds per photon, allows the modelling of short bursts of coherent photons from a laser (50 photons over a period of 4.5 femtoseconds) and the amazing patterns that are produced. To produce coherent photons, we simply assume they are created at the same place (through stimulated emission) and fly off at the speed of light. Producing photons from a more random location with a random phase angle produces an incoherent beam of photons that look very different.

Photon Interference, The Michelson Interferometer

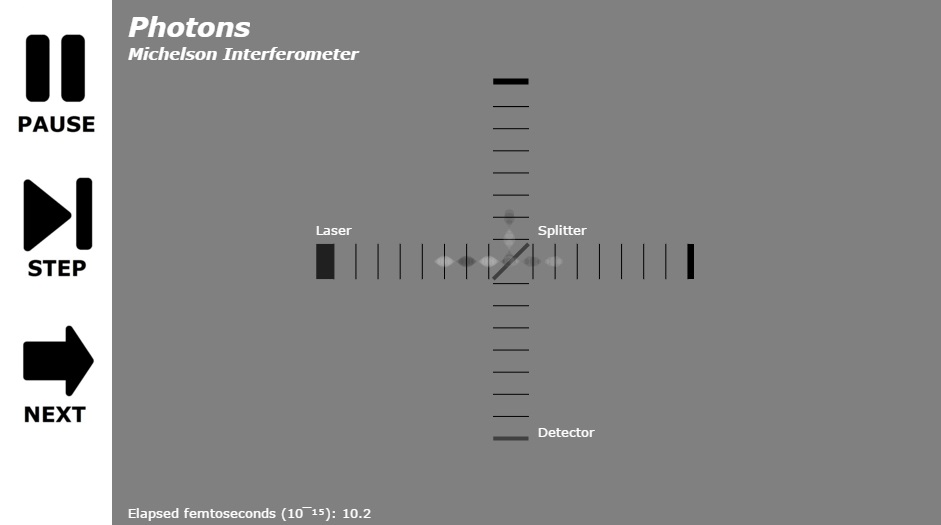
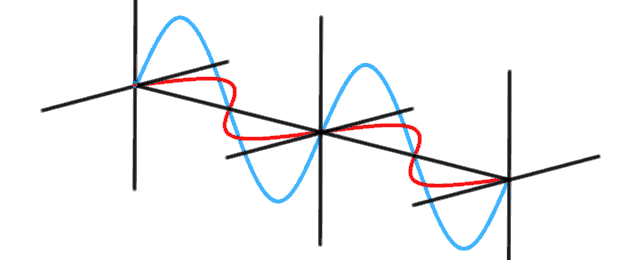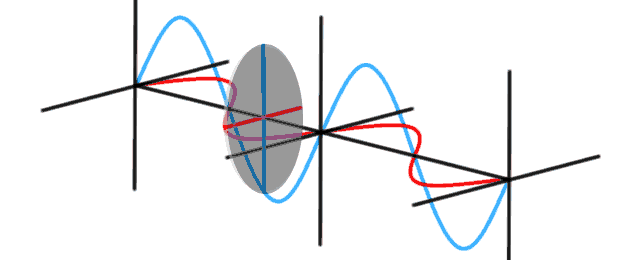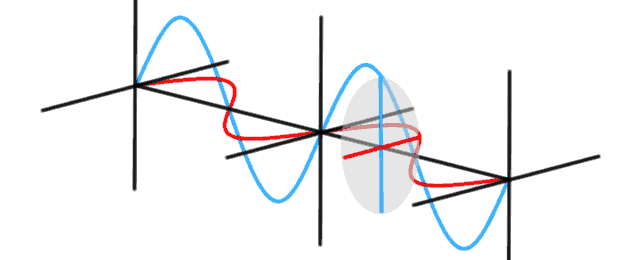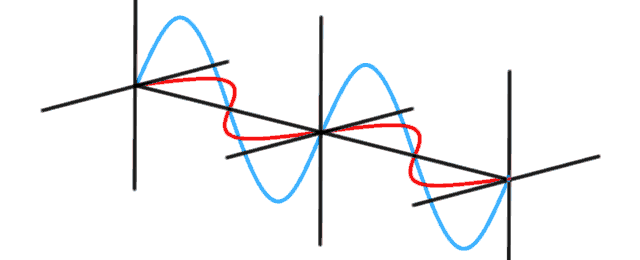
The Michelson interferometer is used to measure tiny differences in length along two different light paths. A laser light source is split into two arms with a beamsplitter. Each arm is reflected back toward the beamsplitter which then combines their amplitudes. The resulting interference pattern that is not directed back toward the source is directed to some type of photoelectric detector or camera. If there is a slight angle between the two returning beams, then an imaging detector will record a sinusoidal fringe pattern. If there is perfect spatial alignment between the returning beams, then there will not be any such pattern but rather a constant intensity over the beam dependent on the difference of the two path lengths.

The model starts with splitting the beam with a beamsplitter. Click to watch photons flow through a Michelson interferometer. Note the beamsplitter is causing the reflected beam to have its phase shifted by 180° while the transmitted beam is not phase shifted. When the beams are recombined, they appear to disappear as the two beams are interfering with each other. Adding a compensating piece of glass shifts the one beam by another 180°, resulting in the two beams now reinforcing each other. Finally, the length of one of the arms in increased by first 1/2 wavelength, then a full wavelength, resulting in first interference, then reinforcement of the wave.

Lasers, Generating Coherent Photons

Lasers generate photons by exciting an electron inside a molecule to a unstable “higher” energy level. When the electron falls back to its normal energy level, a photon is generated with the exact energy of the difference between the two energy levels of the molecule. Many, many photons are generated inside the cavity of the laser, all with the exact same wavelength, but generated in effectively random directions and random locations inside the cavity.

The animation starts with a small group of photons generated at random locations within a small cavity with mirrors on each side. Each photon is labeled so you can view its phase (size) and location. Consider when a large number of photons are generated within the cavity and one of the mirrors is only partially reflective. One end of the laser is “leaking” photons. Most photons are reflected, but if the photon is at a particular point in its oscillation (think small) when it hits the mirror, that photon with pass through. Two laser wavelengths (red, 630nm and 690nm) demonstrates the creation of packets of photons where the wavelength of the photons (oscillation time of the photon) in the packet are the same as the wavelength of the packets themselves (spacing between packets). This effect is independent of the size of the lasing cavity.

The Heisenberg Uncertainty Principle

Heisenberg, like Schrödinger and Planck, viewed the photon in terms of a harmonic oscillator. He addressed the issue of attempting to measure the exact position of a photon at the same time you try to measure the exact energy of a photon. Heisenberg found that it cannot be done. Imagine photons in terms of expanding and contracting bubbles flying through the air. When tiny, you know exactly where the photon is. When it is big, you cant really say where it is, because it appears to be over a wide area. The Planck constant (h), which relates the cycle time (and by extension, how big it gets) of this bubble to the energy it contains, binding the relationship between size and location.

Uncertainty principle: ΔxΔp ≥ h/4π

In this context it makes perfect sense that you can not know both the position (x) and momentum (p), which is energy in the case of a photon, at the same time. It’s either big affecting a wide area, or it’s tiny and only affecting one small area, it cannot be both at the same time.

References

The goal of modelling the photon is to provide mental images of what a photon is all about. With this image, the photon becomes a friendly little guy. When combined with a bunch of other photons, an amazing array of properties emerge.

To view this mathematically, consider Landau & Lifshitz Vol. II. On page 108, the wave equation section talks about electromagnetic waves “in which the field depends only on one coordinate, say x (and on the time). Such waves are said to be plane”. Electromagnetic waves are ever changing “plane waves moving in the positive direction along the X axis”.

In volume IV, page 5, Landau & Lifshitz continue, talking about Quantization of the Free Electromagnetic Field and on page 11, introducing photons:

These formulae enable us to introduce the concept of radiation quanta or photons, which is fundamental throughout quantum electrodynamics. We may regard the free electromagnetic field as an ensemble of particles each with energy ω (= ħω) and momentum k (=nħω/c). The relationship between the photon energy and momentum is as it should be in relativistic mechanics for particles having zero rest-mass and moving with the velocity of light. … The polarization of the photon is analogous to the spin of other particles; …. It is easily seen that the whole of the mathematical formalism developed in §2 is fully in accordance with the representation of the electromagnetic field as an ensemble of photons; it is just the second quantization formalism, applied to the system of photons. …

A photon is a plane wave travelling through space at the speed of light.