Swirling Vortexes
 Hermann von Helmholtz (ca. 1821–1894) was a German physician and physicist who studied fluid dynamics. Specifically, Helmholtz studied vortexes in fluids and developed three theorems which still stand today. The second of Helmholtz’s theorems for vortex dynamics in inviscid fluid states:
Hermann von Helmholtz (ca. 1821–1894) was a German physician and physicist who studied fluid dynamics. Specifically, Helmholtz studied vortexes in fluids and developed three theorems which still stand today. The second of Helmholtz’s theorems for vortex dynamics in inviscid fluid states:
A vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path.
In addition to his theorems in fluid dynamics, Helmholtz’s fundamental theorem of vector calculus states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational (curl-free, longitudinal component) vector field and a solenoidal (divergence-free, transverse component) vector field; this is known as the Helmholtz decomposition.

In the mathematics of group theory, we use orthogonal O(n) and the special orthogonal SO(n) groupings to classify vortexes. Imagine using a computer drawing program like Microsoft Paint. It has five options under the category rotate. They are rotate 90, 180, 270, flip vertical, flip horizontal. Some drawings look the same after a “flip” as they do after a “rotate 180”. But some drawings do not look the same. This is the difference between O(n) groupings and SO(n) groupings.
Group Theory and the Classification of Particles
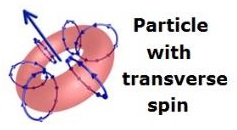 O(3) – Before getting into specific vortexes, think about symmetry. In three dimensions, the O(3) group is all rotations about the origin and all reflections along an axis through the origin. In the O(3) group, particles can have an up or down direction, but reflections must still be in the same O(3) group. These same particles in the O(3) group cannot have a left or right direction, as this would be reversed in a mirror. A particle with only transverse (vertical) spin is a member of an O(3) group and will be the same particle after being reflected in a mirror.
O(3) – Before getting into specific vortexes, think about symmetry. In three dimensions, the O(3) group is all rotations about the origin and all reflections along an axis through the origin. In the O(3) group, particles can have an up or down direction, but reflections must still be in the same O(3) group. These same particles in the O(3) group cannot have a left or right direction, as this would be reversed in a mirror. A particle with only transverse (vertical) spin is a member of an O(3) group and will be the same particle after being reflected in a mirror.
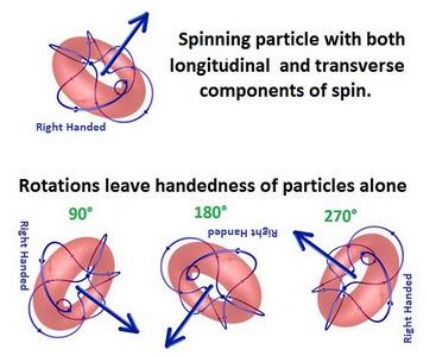 SO(3) – The SO(3) is the group of all rotations about an axis while relections are reversed in a mirror. For the SO(3) group, the fact that the reflection of something in an SO(3) group is not in that same group ensures that when you look at a particle from an SO(3) group, you can tell which division it belongs to. That is the basis for the anti-particle being distinct from the regular particle.
SO(3) – The SO(3) is the group of all rotations about an axis while relections are reversed in a mirror. For the SO(3) group, the fact that the reflection of something in an SO(3) group is not in that same group ensures that when you look at a particle from an SO(3) group, you can tell which division it belongs to. That is the basis for the anti-particle being distinct from the regular particle.
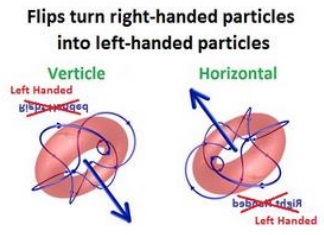 Spinning particles with two components of spin form an SO(3) group. SO(3) group members are classified as either right-handed or left-handed using the right hand rule. You can see from the pictures, that when you bring together one of these SO(3) particles with a mirror image of itself, the spins will conflict with each other no matter what the angle. They will destroy each other.
Spinning particles with two components of spin form an SO(3) group. SO(3) group members are classified as either right-handed or left-handed using the right hand rule. You can see from the pictures, that when you bring together one of these SO(3) particles with a mirror image of itself, the spins will conflict with each other no matter what the angle. They will destroy each other.
The Higgs and Weak Gauge Bosons
 On 4 July 2012, important experimental results were announced at CERN (Conseil Européen pour la Recherche Nucléaire). The discovery was the Higgs Boson with mass of approximately 125 GeV. This amazing event highlights the direct relationship between mathematics and physics, including the predictive power that mathematics gives to physics. The Higgs was predicted solely through the mathematical modelling of the standard model.
On 4 July 2012, important experimental results were announced at CERN (Conseil Européen pour la Recherche Nucléaire). The discovery was the Higgs Boson with mass of approximately 125 GeV. This amazing event highlights the direct relationship between mathematics and physics, including the predictive power that mathematics gives to physics. The Higgs was predicted solely through the mathematical modelling of the standard model.
To match the mathematical properties of the Higgs, the Higgs Boson is modelled as the most basic vortex of swirling energy. The Higgs has only transverse components of spin and is unstable with a lifetime around 1.6×10‾²² seconds.
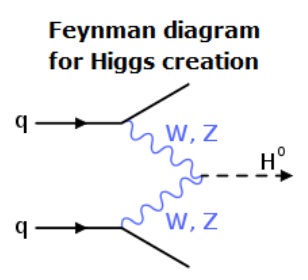
 The Higgs Boson is its own anti-particle, with only a transverse component of spin. The mathematics behind a Higgs Boson decay, tells us that a 125 GeV Higgs, has a 23.3% chance of decaying into a W+/W- particle combination and a 2.9% chance of decaying into a pair of Z bosons. The W bosons have transverse and longitudinal components of spin and are unstable with a lifetime around 3 x 10‾²⁵ seconds. The Z boson has only a longitudinal component of spin.
The Higgs Boson is its own anti-particle, with only a transverse component of spin. The mathematics behind a Higgs Boson decay, tells us that a 125 GeV Higgs, has a 23.3% chance of decaying into a W+/W- particle combination and a 2.9% chance of decaying into a pair of Z bosons. The W bosons have transverse and longitudinal components of spin and are unstable with a lifetime around 3 x 10‾²⁵ seconds. The Z boson has only a longitudinal component of spin.
 The W+ and W- bosons are anti-particles to each other. If you follow the longitudinal spin of the W+ with your fingers, your thumb must point up making the W+ a right-handed particle. If you follow the longitudinal spin of the W- with your fingers, your thumb must point down making the W- a left-handed particle. The Z boson is its own anti-particle and has longitudinal spin with no transverse component of spin.
The W+ and W- bosons are anti-particles to each other. If you follow the longitudinal spin of the W+ with your fingers, your thumb must point up making the W+ a right-handed particle. If you follow the longitudinal spin of the W- with your fingers, your thumb must point down making the W- a left-handed particle. The Z boson is its own anti-particle and has longitudinal spin with no transverse component of spin.
Looking closely at the model, try to visualize the decay of an unstable Higgs. The most likely event, is the breakup of the Higgs into a W+ and a W-. Also, try to visualize the Higgs breaking up into two Z particles, one turning left and one turning right. These are the decays that are seen in particle accelerators like CERN.
It is important to note what happens when these particles interact with other matter. Both the W and Z bosons, being spin 1 particles, change the direction of spin of other particles they hit. A spin up electron (+1/2) will become a down electron (-1/2). The W bosons having a +1 or -1 charge, will change the charge of particles they hit. A +1/3 charge quark will be changed to a -2/3 charged quark if hit by a W- boson.
Wave Equations and the Electron
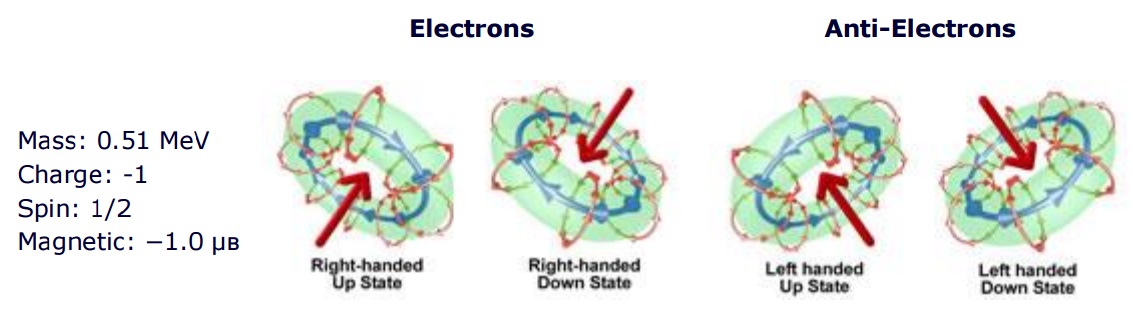
 The mathematical modelling of the electron began in 1922. German physicists Otto Stern and Walther Gerlach shot electrons through a magnetic field and found that half the electrons went up a bit, half the electrons went down a bit and none stayed straight. This clearly demonstrates the principle of spin and that any model of an electron has to have an up and a down state.
The mathematical modelling of the electron began in 1922. German physicists Otto Stern and Walther Gerlach shot electrons through a magnetic field and found that half the electrons went up a bit, half the electrons went down a bit and none stayed straight. This clearly demonstrates the principle of spin and that any model of an electron has to have an up and a down state.
To explain this and many other features of electrons and photons, the physicist Paul Dirac (ca. 1902–1984) represented particles in very new ways. He derived the “Dirac Electron” from earlier wave equations. Wave equations had been around for a long time. The French physicist Jean D’Alembert back in 1750, was the first to study wave equations to model vibrating strings in music. Dirac modelled the electron mathematically as two interacting wave equations. He demonstrated the concept of mass as trapped energy. The model allowed Dirac to derive the mass of the electron and predict the existence of anti-matter.
From Penrose’s Road to Reality (Chapter 25, Section 2):
Dirac’s one equation for a massive particle can be rewritten as two equations for two interacting massless particles, where the Dirac spinor ψ, with its 4 complex components, can be represented, as a pair of 2-spinors αA and βA’ … with a ‘coupling constant’ M describing the strength of the ‘interaction’ between the two.
To visually model the mathematical model of the electron, we get what looks much like a Higgs Boson trapped around a Z boson, but acts very different to both. An electron contains a tiny mass, a strong electrical charge, and a large (relative to other particles) magnetic moment. In an electron, a strong electrical current has trapped an orthogonal magnetic field. One spin around the electrical loop is only 1/2 a spin around the magnetic field. A double spin of 720° is required to return the electron to its original orientation.
![]() An electron is the common decay element of a W- boson. The W- boson is modelled with circulating magnetic and electrical field lines running orthogonal to each other, rotating around each other as they both circulate around the center. The electron breaks this apart. The electrical field lines now spin round in a loop, with the magnetic field lines spinning as a torus orthogonal to the electrical lines.
An electron is the common decay element of a W- boson. The W- boson is modelled with circulating magnetic and electrical field lines running orthogonal to each other, rotating around each other as they both circulate around the center. The electron breaks this apart. The electrical field lines now spin round in a loop, with the magnetic field lines spinning as a torus orthogonal to the electrical lines.
The electron is a lepton and is very stable. The electron has two heavier unstable cousins, with the same charge, spin, and similar magnetic moments. The Muon with a mass of 106 MeV and the Tau with a mass of 1,777 MeV are modelled with additional windings.
Keep in mind, an electron interacting with a W+ Boson, will be flipped into a positron (anti-electron). The boson (with its much higher mass) will reorient the handedness of the red spin compared to the blue spin, turning a right handed particle into a left handed particle. The Z Boson has a chance of turning an up electron into a down electron.
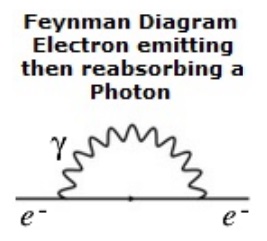 Finally, the amount of force required to flip an electron from an up state to a down state is called the magnetic moment. The magnetic moment of the electron is not quite exactly −1.0 μʙ. There exists a very real (measureable) possibility that as part of the flipping process, a photon will be emitted and reabsorbed by the electron. The mathematical modelling of the magnetic moment of the electron must be adjusted or “renormalized” to take this and other similar interactions into account.
Finally, the amount of force required to flip an electron from an up state to a down state is called the magnetic moment. The magnetic moment of the electron is not quite exactly −1.0 μʙ. There exists a very real (measureable) possibility that as part of the flipping process, a photon will be emitted and reabsorbed by the electron. The mathematical modelling of the magnetic moment of the electron must be adjusted or “renormalized” to take this and other similar interactions into account.
Waves, Particles and the Phase of the Photon
 One thing about energy is that it moves very fast. In one second it is 186,000 miles away. A photon is a packet of energy. In 1807, Thomas Young published his double-slit experiment proving the wave nature of light. James Maxwell (ca. 1831–1879), a Scottish mathematical physicist, wrote “A Treatise on Electricity and Magnetism” in 1873 and formalized the mathematical basis of the electromagnetic wave.
One thing about energy is that it moves very fast. In one second it is 186,000 miles away. A photon is a packet of energy. In 1807, Thomas Young published his double-slit experiment proving the wave nature of light. James Maxwell (ca. 1831–1879), a Scottish mathematical physicist, wrote “A Treatise on Electricity and Magnetism” in 1873 and formalized the mathematical basis of the electromagnetic wave.
Quantum Mechanics forces you to visualize the photon as an oscillating plane wave moving along the Maxwell’s electromagnetic wave. Both the electric and magnetic fields are oscillating positive to negative, in a coordinated manner, orthogonal to each other. The two fields get big, then small, then reverse big, then small, then big, and so on, continuously as the photon moves through space. This action of getting big, then small, then reverse big, then small is one cycle that takes a certain amount of time. This action also acts as a harmonic oscillator and can store energy. The amount of energy in a specific photon is inversely proportional to the amount of time it takes for the photon to grow big then small.
![]() Large energy photons grow large (but not very large) and contract very fast as if they are on a very tight spring. Low energy photons take much longer to grow large, but expand to a much larger size, as if they were on a very loose spring. Based on the connectivity of space itself, the relationship between cycle time and energy is the Planck constant. In 1900, Max Planck, laid out the equations to show a single orange colored photon containing 1.97 eVolts of energy will travel 630 nanometers in one full expansion/contraction cycle. The same 1.97 eVolt photon will take 2 femtoseconds to complete one full cycle.
Large energy photons grow large (but not very large) and contract very fast as if they are on a very tight spring. Low energy photons take much longer to grow large, but expand to a much larger size, as if they were on a very loose spring. Based on the connectivity of space itself, the relationship between cycle time and energy is the Planck constant. In 1900, Max Planck, laid out the equations to show a single orange colored photon containing 1.97 eVolts of energy will travel 630 nanometers in one full expansion/contraction cycle. The same 1.97 eVolt photon will take 2 femtoseconds to complete one full cycle.
The location of the photon along this expansion/contraction cycle is called the “phase” of the photon. A photon in its “large phase” is much more likely to be reflected then a photon in its “small phase”. In a similar manner, a photon in its “small phase” is much more likely to be absorbed by an electron than a photon in its “large phase”. One photon in its “large phase” in the same location with another photon in a “large negative phase”, will not look like a photon at all as one interferes with the other and they cancel each other out. Photons are said to be “coherent” if the phase of their expansion and contraction cycles match.
Complex Numbers, Matrices, and the Polarization of the Photon
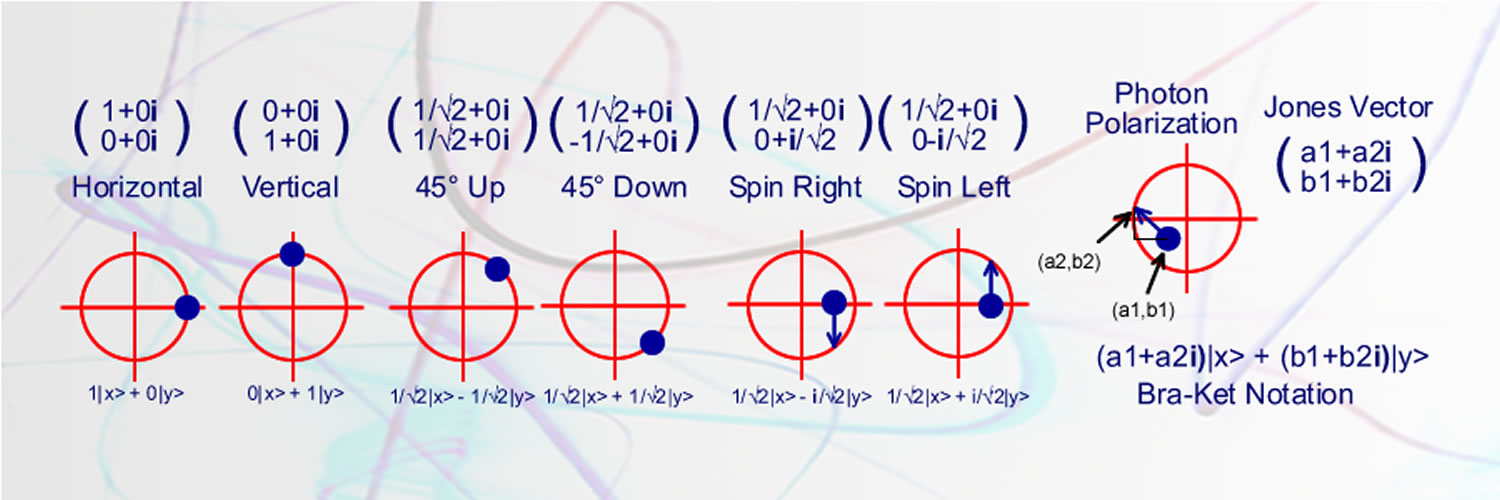
Polarization can be a direction like up or down, left or right. Polarization can also mean spin in a clockwise or counter-clockwise direction. The axis of the electric field may be rotating or spinning in time and we would call the photon spin left or spin right. If the axis appears to stay vertical, we do not know for sure that the axis is vertical. We only know for sure that it has the highest probability of being measured in a vertical direction and zero probability of being measured in a horizontal direction.
The mathematics of polarization starts with the representation of a photon as a vector containing complex numbers (the Jones Vector). To represent this visually, the real part of the variable is where the polarization is right now. The imaginary part represents where the polarization angle is going. Remember, these angles only represent the amplitude of probability. In other words, these angles represent the most likely angle for the polarization to be found. The mathematics captures a particle with a spin axis capable of moving around over time. In addition, the mathematics captures the expansion or contraction of the particle overall.
Using this mathematical representation of the probability of the polarization of a photon highlights the direct and important relationship between mathematics and physics. Matrix multiplication of a vector is now equivalent to an action on the photon. In the real world of physics, the orientation of the photon polarization angle can be manipulated and changed by passing it through a wave plate. In the modelling world of mathematics, multiplication of the Jones vector (representing the photon) by a matrix (used to represent the wave plate), provides the calculation to see what the probability of orientation of the photon is in the real world.
Gauge Symmetries, Quarks and Hadrons
In 1931 Isidor Rabi predicted that the Stern–Gerlach experiment (used to determine the electron was a spin 1/2 particle) could be modified to confirm the properties of protons and neutrons in the atomic nucleus. Rabi built a molecular beam apparatus and employed a weak magnetic field to detect the nuclear spin of sodium. When the experiment was conducted, four beamlets were found, indicating that the nuclear spin of sodium was 3⁄2. To model his findings, Rabi used the work of Joseph Larmor.
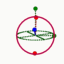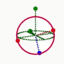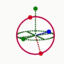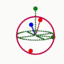 Joseph Larmor (ca. 1857–1942) was a physicist and mathematician who made substantial contributions to the view of matter as spinning vortexes. Where mass is involved, Larmor laid the groundwork for mathematically modelling the concepts of spin, precession and coupling for nucleons. Coupling the up or down energy states of multiple spin 1/2 particles allows for mathematical modelling of more complex particle spin. One spin 1/2 particle will go up or down. Two spin 1/2 particles coupled together (spin 1) can go in three different directions. Three spin 1/2 particles coupled together (spin 3/2) will form 4 beamlets, just like the Rabi experiment.
Joseph Larmor (ca. 1857–1942) was a physicist and mathematician who made substantial contributions to the view of matter as spinning vortexes. Where mass is involved, Larmor laid the groundwork for mathematically modelling the concepts of spin, precession and coupling for nucleons. Coupling the up or down energy states of multiple spin 1/2 particles allows for mathematical modelling of more complex particle spin. One spin 1/2 particle will go up or down. Two spin 1/2 particles coupled together (spin 1) can go in three different directions. Three spin 1/2 particles coupled together (spin 3/2) will form 4 beamlets, just like the Rabi experiment.
With the development of high speed colliders the model becomes far more complex. An electron modelled as a special unitary SU(2) gauge symmetry group, only deals with two properties, magnetic up or down and spin left handed or right handed. The combinations of properties generate only four different particles. With hadrons, there is a literal “particle zoo” with a multitude hadrons discovered. In 1964, The quark model was proposed by physicists Murray Gell-Mann and George Zweig using special unitary SU(3) flavor symmetry. SU(3) symmetry has three properties, often labeled red plus or minus, green plus or minus and blue plus or minus. SU(3) symmetry gives you eight different ways of binding quarks together through gluons.
To visually present the SU(3) group, we use three properties: specifically magnetic up or down; spin left handed or right handed; and, flow in or out.
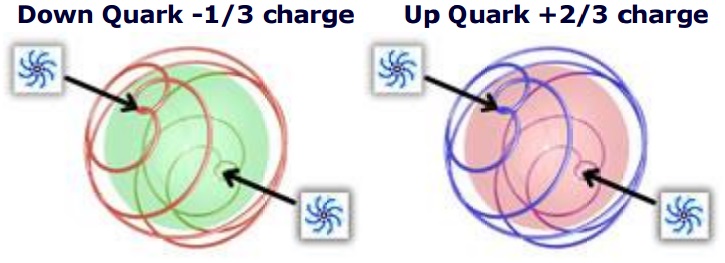 Close your eyes for a moment and use your imagination. Imagine a large empty sphere, maybe like a big beach ball. Looking closer, notice the surface of the beach ball is actually made up of several layers of different beach balls. Not only that, the layers are able to spin independent of each other with one beach ball spinning one way and the beach ball just inside it spinning in a different direction! Finally, notice the surface of any one beach ball. It’s spinning in two directions. Put your finger on a point of the sphere and track it. You find your finger not only rotating around the sphere, but also, up and down directly through the north and south poles. The poles are spinning very fast and different layers can “couple” together at the poles. OK, time to open your eyes.
Close your eyes for a moment and use your imagination. Imagine a large empty sphere, maybe like a big beach ball. Looking closer, notice the surface of the beach ball is actually made up of several layers of different beach balls. Not only that, the layers are able to spin independent of each other with one beach ball spinning one way and the beach ball just inside it spinning in a different direction! Finally, notice the surface of any one beach ball. It’s spinning in two directions. Put your finger on a point of the sphere and track it. You find your finger not only rotating around the sphere, but also, up and down directly through the north and south poles. The poles are spinning very fast and different layers can “couple” together at the poles. OK, time to open your eyes.
Quarks are large empty 3D spinning spherical shells with both longitudinal and transverse components of spin. Quarks colored blue symbolize a +2/3 charge and red symbolizes a -1/3 charge. When layered, these spheres make up Mesons and Baryons. Mesons have two layers of quark shells, Baryons have three layers. Protons and Neutrons (both three layered Baryons) are the final, and most noticeable of the layered quarks. Quark shells are able to stack or layer together with the help of gluons. Gluons act both as “lubricant” between quark layers and as special “taps” that allow energy to flow in or out of a particular region.
 An important attribute of spin on a quark is what happens at the poles. If you follow the spin of an individual point on the surface of a shell modeled this way, you will notice it goes directly through both the north and the south pole of the quark on every turn. This means a lot of paths are directly converging and diverging at the poles. To accommodate this we assume the converging lines are coming in either above or below the outgoing diverging lines.
An important attribute of spin on a quark is what happens at the poles. If you follow the spin of an individual point on the surface of a shell modeled this way, you will notice it goes directly through both the north and the south pole of the quark on every turn. This means a lot of paths are directly converging and diverging at the poles. To accommodate this we assume the converging lines are coming in either above or below the outgoing diverging lines. 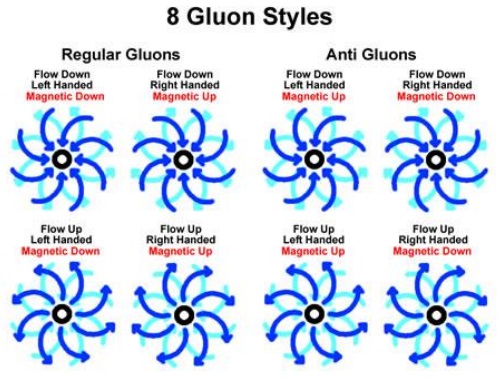 Also, the left or right handedness of the poles tells us which way the magnetic field is pointing for both regular and anti-quarks.
Also, the left or right handedness of the poles tells us which way the magnetic field is pointing for both regular and anti-quarks.
The properties of the gluon are called its color charge. There are three color charges, specifically spin (clockwise or counter clockwise) magnetic direction (up or down) and flow (in or out), making 8 unique gluons. The “Color charge” rules are detailed in quantum chromodynamics (QCD), and are a basis for the interaction of quarks and gluons to form more complex elements.
Conclusion
Visual imaging of the mathematical modelling of elementary particles of the Standard Model significantly improves the usefulness of these models. Different visual images within the same mathematical framework can co-exist until some aspect of the imaging is shown to be inconsistent with the real world. These images must then be corrected, removed or placed within a specific scope. The massive particles built from a variety of swirling energy vortex styles exhibit the same properties seen in particle colliders. Massless particles expanding and contracting as they zip through space do the same unusual things waves do. These images provide a basis to build an understanding of much deeper concepts and help foster predictions that will lead to a deeper understanding of the world around us.
Epicurus (ca. 341–270 BC) in a letter to Pythocles:
When one accepts one theory and rejects another which is equally consistent with the phenomenon in question, it is clear that one has thereby blundered out of any sort of proper physics and fallen into mythology.
Extended Animations and Videos
Visualizing Vortexes
- Make vortexes in your backyard pool, Crazy pool vortex, Nov 22, 2014, Physics Girl
https://www.youtube.com/watch?v=pnbJEg9r1o8 - Whales making vortexes in the ocean, Extraordinary Toroidal Vortices, Feb 12, 2010, Evasius
https://www.youtube.com/watch?v=mHyTOcfF99o - Two smoke rings collide. The interaction of a pair of higgs bosons, creating a quark/anti-quark pair
http://www.animatedphysics.com/Particle_Zoo/video.html
Understanding Spin
- Spin 1/2 model, The Gyroscope, Jan 2, 2009, ScienceOnline
https://www.youtube.com/watch?v=cquvA_IpEsA - Spin 3/2 model, The Gyrocube, Apr 9, 2013, edguy99
http://youtu.be/oY6uGMhW1_4
Spinning Spheres
- Tracking spin on the surface of a sphere, AnimatedPhysics
http://www.animatedphysics.com/videos/spinningblochsphere.htm - Larmor Frequency on a spinning sphere, AnimatedPhysics
http://www.animatedphysics.com/videos/larmorfrequency.htm - Rabi Oscillations or spin flips to match an external field, AnimatedPhysics
http://www.animatedphysics.com/videos/rabioscillations.htm
Massless particles – Photons
- Photons, relationship between energy and wavelength, AnimatedPhysics
http://www.animatedphysics.com/games/photon_oscillator.htm - Burst of 50 photons over 4.5 femtoseconds, AnimatedPhysics
http://www.animatedphysics.com/games/photon_cavity.htm
Massive Particles – Protons, Neutrons and Electrons
- Protons and Neutrons, three layered quarks, AnimatedPhysics
http://www.animatedphysics.com/videos/nucleons.htm - Electrons and the axis of emitted photons, AnimatedPhysics
http://www.animatedphysics.com/videos/electrons.htm