A wealthy man wants to predict the outcome of a horse race. Not knowing how, he looks for some expert advice. He talks to a biologist who says he could genetically engineer an unbeatable racehorse, but it would take a long time and lots and lots of money. He talks to a statistician who says he could predict the outcome of any race, for much less money, but he would only be right part of the time. Finally, he talks to a physicist, who says he can do it cheap and simple. Wow, says the wealthy man, how do you do it? The physicist reports, “I have made several simplifying assumptions: first, let each horse be a perfect rolling sphere… ”

This oft repeated joke sums up the thinking of George Box (18 October 1919 – 28 March 2013), one of the great statistical minds of the 20th century, who wrote that “essentially, all models are wrong, but some are useful”. In his words

Now it would be very remarkable if any system existing in the real world could be exactly represented by any simple model. However, cunningly chosen parsimonious models often do provide remarkably useful approximations. For example, the law PV = RT relating pressure P, volume V and temperature T of an “ideal” gas via a constant R is not exactly true for any real gas, but it frequently provides a useful approximation and furthermore its structure is informative since it springs from a physical view of the behavior of gas molecules.

For such a model there is no need to ask the question “Is the model true?”. If “truth” is to be the “whole truth” the answer must be “No”. The only question of interest is “Is the model illuminating and useful?”.

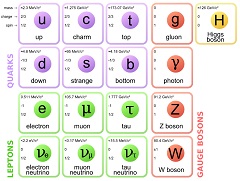
The next entry will lead you through an animation model of the particles of the standard model. Using swirling vertexes of connected space, particles matching the quantum properties of the fundamental particles.

There are a lot of illustrations to follow. The illustrations are here to help the reader build a mental image of the mathematical objects presented. This mental image helps the reader better remember facts about the particles (ie. gluons have 8 different styles). This mental image allows the reader to better anticipate what happens over time (ie. Beta decay, where a proton and an electron are made from a neutron). Lastly, this mental image is very important in human understanding of the relationship between mathematics, physics and the real world.