A photon travels through the air as if it had a specific axis of spin called polarization. We know this is true because certain crystals will send photons in different directions depending on their polarization. By detecting which way the photon went, we know something about the polarization of the photon.

Researchers at the National Institute of Standards and Technology (NIST) in a recent paper, A strong loophole-free test of local realism, have proved “spooky actions at a distance” through the statistics of measuring entangled photons at specific angles. The test starts with a photon with known polarization. A crystal splits the photon into two, each of which retains the polarization of the original photon. The photons with matching polarization are sent off in two different directions to be measured by two different people. If the two people measure the photons along the vertical or horizontal directions they get matching results. This is not surprising since the photons were created with matching polarization.

Spooky Actions at a Distance

What the researchers tested was to measure the orientation of the photon slightly off the horizontal or vertical position. Results were compared and plugged into a statistical Bell type equation  to prove “spooky actions at a distance”. Specifically, it appears what one person measures as the polarity of the photon, could depend on which setting the other person has on his detector, even though it is a long way away and makes no sense why the second persons setting should affect the first persons reading.

According to Albert Einstein and his colleagues Boris Podolsky and Nathan Rosen (“EPR”) there were two possible explanations. Either there was some interaction between the particles (even though they were separated) or the information about the outcome of all possible measurements was already present in both particles. Unfortunately the “hidden variables” that would describe the properties of the particles and their interactions were not found and John Stewart Bell designed a proof (depending on a series of assumptions) that would prove that “hidden variables” could not explain a photons behavior.

John Stewart Bell and Quantum Mechanics

John Bell starts by laying out the concept of hidden variables

It has been argued that quantum mechanics is not locally causal and cannot be embedded in a locally causal theory. That conclusion depends on treating certain experimental parameters, typically the orientations of polarization filters, as free variables. But it might be that this apparent freedom is illusory. Perhaps experimental parameters and experimental results are both consequences, or partially so, of some common hidden mechanism. Then the apparent non-locality could be simulated.

And concludes in “On the Einstein-Podolsky-Rosen Paradox” with

But if [a hidden variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local. This is what the theorem says.

Bell derived the inequality ρ(a,c) – ρ(a,c) – ρ(a,c) ≤ 1 where ρ is the correlation between measurements of the spins of the pair of particles and a, b and c refer to three arbitrary settings of the two analyzers. It is a version of this inequality that the researchers have found is violated by quantum mechanics.

Photon Models Governed by Bell’s Inequality

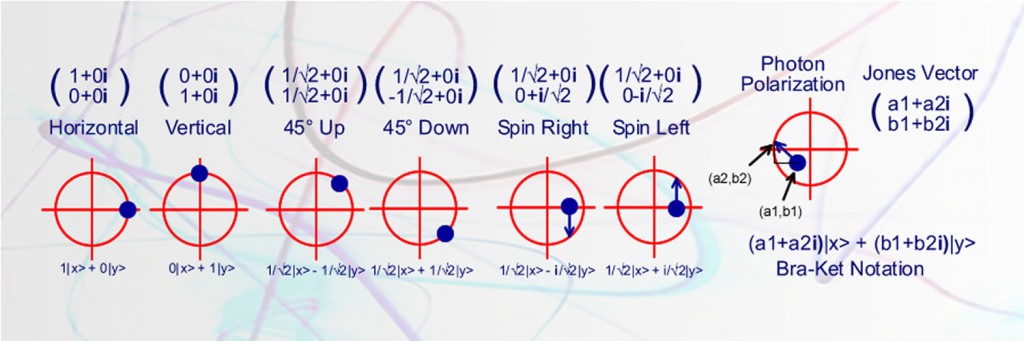
Bell’s inequality is however restricted to the rather special case in which the outcomes on both sides of the experiment are always exactly correlated whenever the analyzers are parallel. An example of this type of model would see each photon having a polarization angle λ. When a photon meets a polarizer set to an angle γ , it will always register as vertical if λ is closer to γ than to γ + π/2, i.e.,

• if |γ − λ| ≤ π/4 then vertical
• if |γ − λ| > 3π/4 then vertical
• horizontal otherwise.

Photon Models Not Governed by Bell’s Inequality

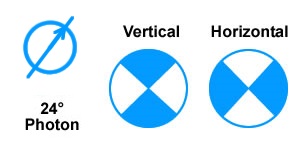
Any model that introduces a statistical nature to the measurement of photon polarization is not governed by Bell’s inequality. Consider a photon model where the spin axis rotates around a polarization angle in a process called precession. Each photon needs two variables to describe it. A precession angle of ø that varies from 0° to 45°, rotating around an axis angle of λ. From the front, the photon polarization angle will appear to wobble back and forth between λ + ø and λ – ø.   Now, when a photon meets a polarizer set to an angle γ, it will not always register the same. When a photon meets a polarizer set to an angle γ, it has a better chance to register as vertical if λ is closer to γ than to γ + π/2, i.e.,

• Chance of vertical measurement = (cos((γ − λ)*2)+1)/2
• Chance of horizontal measurement = (cos((γ − λ + π/2)*2)+1)/2

Now consider some angles. A horizontal photon has a 100% chance of getting through a horizontal polarizer. A vertical photon has 0% chance of getting through a horizontal polarizer. A photon with a polarization angle of 45° has a 50% chance of getting through a horizontal polarizer and a 50% chance of getting through a vertical polarizer. Finally, a photon with polarization angle of 22.5° has a 85% chance of getting through a horizontal polarizer and a 15% chance of getting through a vertical polarizer.

The Statistical Nature of Photon Polarization

The recent experiments that have closed all the loopholes in Bell’s inequalities provide an important point in the understanding of the nature of the real world. Our current methods of measuring polarization yield fundamentally probabilistic results and any model must account for this. High speed precession of the spin axis of the photon provides the hidden variables needed to model “Spooky Actions at a Distance”.

Click to view a detailed model of experimental results dealing with entangled photons, non locality and Bell inequalities based on the work of Dietrich Dehlinger and M. W. Mitchell.